INQUIRY ACTIVITY SUMMARY
1. The Pythagorean identity, sin^2x+cos^2x=1, comes from the Pythagorean Theorem. If we arranged the Pythagorean theorem using x, y, and z, we would get x^2 + y^2 = r^2. And, if we made this equation equal one, we would have to divide everything by r^2. So, we would get: (x^2)/(r^2) + (y^2)/(r^2) = 1. We already know the trig ratio for cosine is x/r and the ratio for sine is y/r. So, (x^2)/(r^2)= cos^2 and (y^2)/(r^2) = sin^2. Therefore, for our final answer, we would get: cos^2 + sin^2 = 1, our Pythagorean theorem. Look at the pictures below for a visual. Also, we can prove this by plugging in values from the unit circle. The example below uses the coordinates of the 30 degree reference angle: (rad 3/2, 1/2).
2. To derive the two remaining Pythagorean Identities from sin^2x+cos^2x=1, divide it by cos^2x and sin^2x. When you divide it by cos^2x, you shuold get 1 + tan^2x = sec^2x. Then, when you divide it by sin^2x, you should get 1 + cot^2x = csc^2x. Look at the pictures below to see, step by step, how I got them.
INQUIRY ACTIVITY REFLECTION
1. "The connections that I see between Units N, O, P, and Q so far are:" how the Pythagorean identities are derived from the Pythagorean Theorem (x^2 + y^2 = r^2) -> ( x^2/r^2 + y^2/r^2 = 1) ->(cos^2x + sin^2 = 1) and how the reciprocal and ratio identities are derived from the trig ratios (cotx= cosx/sinx) -> (x/y) / (y/r) = x/y
2. "If I had to describe trigonometry in THREE words, they would be:" triangles, identities, and ratios.
Showing posts with label I/D. Show all posts
Showing posts with label I/D. Show all posts
Wednesday, March 19, 2014
Tuesday, March 4, 2014
I/D2: Unit O - How can we derive the patterns for our special right triangles?
INQUIRY ACTIVITY SUMMARY
1. We can derive the 30-60-90 triangle from an equilateral triangle with a side length of 1 by using the information we already know about equilateral triangles. An equilateral triangle has the same length on all sides (1) and has equal degrees as well (60 degrees). If we cut this triangle down the middle, the side length that is cut will become 1/2 for the 30 degree angle. And, the degree formed will become a 90 degree angle, which will have a opposite side length of 1 still. Since we know the hypotenuse and one leg, we can use the Pythagorean Theorem to solve for the second leg. The work for this is shown below. In the end, we get the leg to be rad 3/2. If we were to multiply all these side lengths by 2, to make the numbers easier to work with, we would get: 1 (30 degree), 2 (90 degree), and rad 3 (60 degree). If we were to replace these values with n, we would get: n, 2n, and n rad 3. The "n" is a variable that depends on the triangle and shows the relation between the sides, the ratio.
2. We can derive the 45-45-90 triangle from a square with a side length of 1 by using the information we already know about squares. All the sides are equal and all the angles are 90 degrees. Therefore, if we cut the square along its diagonal, the two legs of the triangle formed will remain 1. Also, the right angle will be cut in half, so the angles would be 45 degrees. In order to find the length of the hypotenuse, we can use the Pythagorean Theorem. The work shown below gives the answer of c= rad 2. Therefore, if we get our sides as: 1 (45 degree), 1 (45 degree), rad 2 (90 degree). If we replace the values with n, we get: n, n, and n rad 2. The "n" is a variable that depends on the triangle and displays the ratio of the sides, or, in other words, the relationship between them.
INQUIRY ACTIVITY REFLECTION
1. "Something I never noticed before about special right triangles is:" how they are derived from basic shapes, follow the same rules, and make logical sense as well as mathematical.
2. "Being able to derive these patterns myself aids in my learning because:" it allows me to fully comprehend where these values come from, not just accept them blindly.
1. We can derive the 30-60-90 triangle from an equilateral triangle with a side length of 1 by using the information we already know about equilateral triangles. An equilateral triangle has the same length on all sides (1) and has equal degrees as well (60 degrees). If we cut this triangle down the middle, the side length that is cut will become 1/2 for the 30 degree angle. And, the degree formed will become a 90 degree angle, which will have a opposite side length of 1 still. Since we know the hypotenuse and one leg, we can use the Pythagorean Theorem to solve for the second leg. The work for this is shown below. In the end, we get the leg to be rad 3/2. If we were to multiply all these side lengths by 2, to make the numbers easier to work with, we would get: 1 (30 degree), 2 (90 degree), and rad 3 (60 degree). If we were to replace these values with n, we would get: n, 2n, and n rad 3. The "n" is a variable that depends on the triangle and shows the relation between the sides, the ratio.
2. We can derive the 45-45-90 triangle from a square with a side length of 1 by using the information we already know about squares. All the sides are equal and all the angles are 90 degrees. Therefore, if we cut the square along its diagonal, the two legs of the triangle formed will remain 1. Also, the right angle will be cut in half, so the angles would be 45 degrees. In order to find the length of the hypotenuse, we can use the Pythagorean Theorem. The work shown below gives the answer of c= rad 2. Therefore, if we get our sides as: 1 (45 degree), 1 (45 degree), rad 2 (90 degree). If we replace the values with n, we get: n, n, and n rad 2. The "n" is a variable that depends on the triangle and displays the ratio of the sides, or, in other words, the relationship between them.
INQUIRY ACTIVITY REFLECTION
1. "Something I never noticed before about special right triangles is:" how they are derived from basic shapes, follow the same rules, and make logical sense as well as mathematical.
2. "Being able to derive these patterns myself aids in my learning because:" it allows me to fully comprehend where these values come from, not just accept them blindly.
Saturday, February 22, 2014
I/D# 1: Unit N - How do SRT and UC relate?
INQUIRY ACTIVITY SUMMARY
1. For a 30 degree special right triangle, the rule is
Therefore, when we simply the hypotenuse to "1," by dividing each value by 2n, we get: r = 1 (hypotenuse), x = √3/2 (horizontal), and y = 1/2 (vertical). The work for dividing is shown below.
.JPG)
.JPG)
After finding the values, we can plot the special triangle onto a coordinate plane. If this triangle is put in the first quadrant, its coordinates would be (0,0); (√3/2,1/2); (√3/2,0).
2. For a 45 degree special right triangle, the rule is
When we simply the hypotenuse to "1," by dividing by n√2, we get: r = 1 (hypotenuse), x = √2/2 (horizontal), and y = √2/2 (vertical). The work for dividing is shown below.

After finding the values, we can plot the special triangle onto a coordinate plane. If this triangle is put in the first quadrant, its coordinates would be (0,0); (√2/2,√2/2); (√2/2,0).
3. For a 60 degree special right triangle, the rule is the same as a 30 degree special triangle:
So, when we simply the hypotenuse to "1," by dividing each value by 2n, we get: r = 1 (hypotenuse), x = 1/2 (horizontal), and y = √3/2 (vertical). This is very similar to the 30 degree triangle. The only difference is that the x and y values are switched. The work for dividing is shown below.
 After
finding the values, we can plot the special triangle onto a coordinate
plane. If this triangle is put in the first quadrant, its coordinates
would be (0,0); (1/2, √3/2); (1/2, 0).
After
finding the values, we can plot the special triangle onto a coordinate
plane. If this triangle is put in the first quadrant, its coordinates
would be (0,0); (1/2, √3/2); (1/2, 0).
4. This activity helped me derive the Unit Circle by showing me that the Unit Circle is just made up of special right triangles. The 30, 45, and 60 degree triangles have the same coordinates as the first quadrant of the Unit Circle. And, if we use the reference angles of these triangles, we can get the coordinates of the remaining points on the Unit Circle.
5. The triangle in this activity lies in the first quadrant. However, in the second quadrant, the x values are negative. In the third quadrant, both the x and y values are negative. Finally, in the fourth quadrant, the y values are negative. The first image shows a 30 degree special triangle in Quadrant II, notice how the x value is negative. The second image portrays a 45 degree special triangle in Quadrant III, notice how both the x and y value of the coordinates are negative. Finally, the third picture displays a 60 degree special triangle in Quadrant IV, notice how the y value is negative.
INQUIRY ACTIVITY REFLECTION
1. "The coolest thing I learned from this activity was:" that the triangles are in all the quadrants. They are just flipped around, so the coordinate signs change.
2. "This activity will help me in this unit because:" it helped me memorize the unit circle
3. "Something I never realized before about special right triangles and the unit circle is:" that the unit circle is completely made up of special triangles.
1. For a 30 degree special right triangle, the rule is
30°
|
60°
|
90°
|
n
|
n√3
|
2n
|
Therefore, when we simply the hypotenuse to "1," by dividing each value by 2n, we get: r = 1 (hypotenuse), x = √3/2 (horizontal), and y = 1/2 (vertical). The work for dividing is shown below.
.JPG)
.JPG)
After finding the values, we can plot the special triangle onto a coordinate plane. If this triangle is put in the first quadrant, its coordinates would be (0,0); (√3/2,1/2); (√3/2,0).
2. For a 45 degree special right triangle, the rule is
45°
|
45°
|
90°
|
n
|
n
|
n√2
|
When we simply the hypotenuse to "1," by dividing by n√2, we get: r = 1 (hypotenuse), x = √2/2 (horizontal), and y = √2/2 (vertical). The work for dividing is shown below.

After finding the values, we can plot the special triangle onto a coordinate plane. If this triangle is put in the first quadrant, its coordinates would be (0,0); (√2/2,√2/2); (√2/2,0).
3. For a 60 degree special right triangle, the rule is the same as a 30 degree special triangle:
30°
|
60°
|
90°
|
n
|
n√3
|
2n
|
So, when we simply the hypotenuse to "1," by dividing each value by 2n, we get: r = 1 (hypotenuse), x = 1/2 (horizontal), and y = √3/2 (vertical). This is very similar to the 30 degree triangle. The only difference is that the x and y values are switched. The work for dividing is shown below.
 After
finding the values, we can plot the special triangle onto a coordinate
plane. If this triangle is put in the first quadrant, its coordinates
would be (0,0); (1/2, √3/2); (1/2, 0).
After
finding the values, we can plot the special triangle onto a coordinate
plane. If this triangle is put in the first quadrant, its coordinates
would be (0,0); (1/2, √3/2); (1/2, 0). 4. This activity helped me derive the Unit Circle by showing me that the Unit Circle is just made up of special right triangles. The 30, 45, and 60 degree triangles have the same coordinates as the first quadrant of the Unit Circle. And, if we use the reference angles of these triangles, we can get the coordinates of the remaining points on the Unit Circle.
5. The triangle in this activity lies in the first quadrant. However, in the second quadrant, the x values are negative. In the third quadrant, both the x and y values are negative. Finally, in the fourth quadrant, the y values are negative. The first image shows a 30 degree special triangle in Quadrant II, notice how the x value is negative. The second image portrays a 45 degree special triangle in Quadrant III, notice how both the x and y value of the coordinates are negative. Finally, the third picture displays a 60 degree special triangle in Quadrant IV, notice how the y value is negative.
INQUIRY ACTIVITY REFLECTION
1. "The coolest thing I learned from this activity was:" that the triangles are in all the quadrants. They are just flipped around, so the coordinate signs change.
2. "This activity will help me in this unit because:" it helped me memorize the unit circle
3. "Something I never realized before about special right triangles and the unit circle is:" that the unit circle is completely made up of special triangles.
Subscribe to:
Posts (Atom)





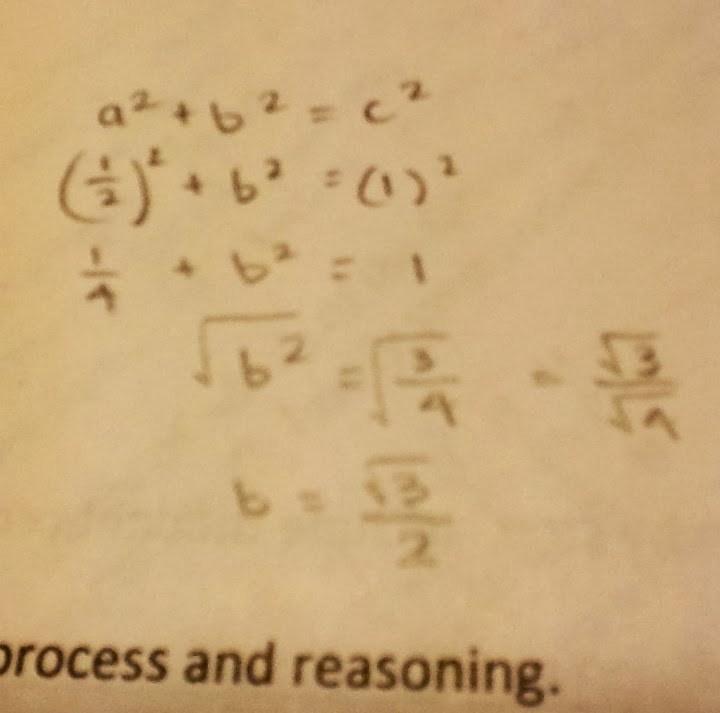




.JPG)

.JPG)
.JPG)
.JPG)
.JPG)
.JPG)