1. We can derive the 30-60-90 triangle from an equilateral triangle with a side length of 1 by using the information we already know about equilateral triangles. An equilateral triangle has the same length on all sides (1) and has equal degrees as well (60 degrees). If we cut this triangle down the middle, the side length that is cut will become 1/2 for the 30 degree angle. And, the degree formed will become a 90 degree angle, which will have a opposite side length of 1 still. Since we know the hypotenuse and one leg, we can use the Pythagorean Theorem to solve for the second leg. The work for this is shown below. In the end, we get the leg to be rad 3/2. If we were to multiply all these side lengths by 2, to make the numbers easier to work with, we would get: 1 (30 degree), 2 (90 degree), and rad 3 (60 degree). If we were to replace these values with n, we would get: n, 2n, and n rad 3. The "n" is a variable that depends on the triangle and shows the relation between the sides, the ratio.
2. We can derive the 45-45-90 triangle from a square with a side length of 1 by using the information we already know about squares. All the sides are equal and all the angles are 90 degrees. Therefore, if we cut the square along its diagonal, the two legs of the triangle formed will remain 1. Also, the right angle will be cut in half, so the angles would be 45 degrees. In order to find the length of the hypotenuse, we can use the Pythagorean Theorem. The work shown below gives the answer of c= rad 2. Therefore, if we get our sides as: 1 (45 degree), 1 (45 degree), rad 2 (90 degree). If we replace the values with n, we get: n, n, and n rad 2. The "n" is a variable that depends on the triangle and displays the ratio of the sides, or, in other words, the relationship between them.
INQUIRY ACTIVITY REFLECTION
1. "Something I never noticed before about special right triangles is:" how they are derived from basic shapes, follow the same rules, and make logical sense as well as mathematical.
2. "Being able to derive these patterns myself aids in my learning because:" it allows me to fully comprehend where these values come from, not just accept them blindly.

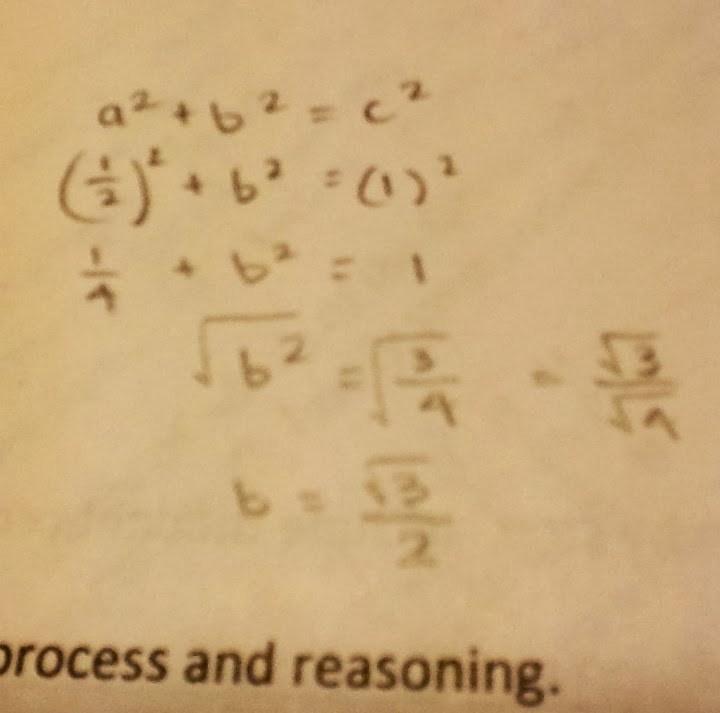



No comments:
Post a Comment