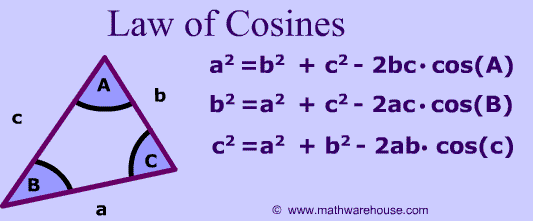BQ# 1: Unit P - Oblique Triangles, Law of Sines & Cosines, and Area

3. Law of Cosines

http://www.mathwarehouse.com/trigonometry/images/law-of-cosines/law-of-cosines-formula-and-picture2.gif

We need law of cosines to find certain sides or angles of an oblique triangle when we are given SSS (side-side-side) or SAS (side-angle-side). If we are given an oblique triangle and cut it down the middle of the base, we can create 2 right triangles (see pic below). 

Then, we can label the line h, for height. Now let's say we need to find the length of side a. We can use the distance formula, but to do that, we need the coordinates of angle B and angle C. If cosA=d/c, then d=ccosA. And, if sinA=h/c, then h=csinA. Therefore, angle B will be (ccosA, csinA). For angle C, b is the x value and 0 is the y value (b,0). Now that we have our two coordinates, we can plug these values in the  distance formula (see right): a^2=(ccosA-b^2)^2 + (csinA-0)^2. We need to FOIL (ccosA-b^2)^2 and simolify (csinA-0)^2. Then, we need to factor out c^2 from c^2sin^2A and c^cos^2A. (cos^2 + sin^2A) =1 (This is a trigonometric identity.) Thus, when we take the remaining numbers (highlighted in green), we obtain a^2=b^2+c^2-2bccosA, which is our Law of Cosines formula, which can be rearranged in three different ways (see 1st image).
Moreover, it is similar to the Pythagorean Theorem because the Pythagorean theorem is derived from the law of cosines.  If one of the angles is 90 degrees, then the cos(90)= 0. Therefore, we can leave out the -2bccosC, and it simplifies to a^2+b^2 = c^2.

5. Area Formulas

All three area formulas will work. They just use different values.

References:
http://www.mathwarehouse.com/trigonometry/images/law-of-cosines/law-of-cosines-formula-and-picture2.gif